中文 | English

高级计量经济学

中文> 正文

Eviews方程参数估计方法汇总

作者：时间：2022-09-03 点击数：

数量经济学 2022-09-02 22:12

1、LS最小二乘法，可以用于线性回归模型、ARMA等模型
2、TSLS两阶段最小二乘法
3、GMM广义矩估计方法
4、ARCH自回归条件异方差，还可以估计其他各种ARCH模型，如 GARCH、T- GARCH
5、BINARY用于估计二元选择模型，包括 Logit、 Probit和 Extreme value模型
6、ORDERED用于估计有序选择模型
7、CENSORED用于估计删截模型
8、COUNT用于估计计数模型
9、OREG分位数回归分析方法
10、GLM义线性模型分析方法
11、STEPLS分段最小二乘分析方法
12、ROBUSTLS稳健最小二乘分析方法
13、HECKIT赫克曼备择模型
14、BREAKLS带断点的最小二乘分析方法
15、THRESHOLD门限回归分析
16、SWTCHREG转换回归
17、ARDL自回归分布滞后模型
18、IDAS混合数据抽样

TSLS两阶段最小二乘法

一个典型的线性回归模型:y= β0 + β1x1+ βX + ε(1)，这里y为被解释变量，x1为自变量，或者解释变量，也即“因”。大写的 X为外生控制项向量( 也即一组假定为外生的其他控制变量，例如年龄、性别等等) ，ε则为误差项。如果ε与x1不相关，那么我们可以利用OLS 模型对方程进行无偏估计。

然而，如果一个重要变量x2被模型(1) 遗漏了，且x1和x2也相关，那么对β1的OLS 估计值就必然是有偏的。

此时，x1被称作“内生”的解释变量，这就是 “内生性”问题。遇到“内生性”问题肿木办？有一个方法就是找工具变量Z。

如果存在内生性，则称解释变量为 “内生变量”（endogenousvariable）；反之，则称为 “外生变量”（exogenous variable）。

内生性的严重后果是使得 OLS估计量不一致（inconsistent），即无论样本容量多大，OLS 估计量也不会收敛至真实的参数值。

在计量经济学中，把所有与扰动项相关的解释变量都称为“内生变量”。这与一般经济学理论中的定义有所不同。1。与误差项相关的变量称为内生变量(endogenous variable)。2。与误差项不相关的变量称为外生变量(exogenous variable)。

二阶段最小二乘法Eviews操作介绍：二阶段最小二乘法的第一阶段就是利用原模型的内生解释变量对工具变量进行OLS，得到解释变量的拟合值；第二步，利用得到解释变量的拟合值对原模型进行最小二乘法，从而得到方程模型的估计值，这样就可以消除内生性的影响。

原文阅读：一文读懂内生性问题之二阶段最小二乘法（TSLS）Eviews操作

THRESHOLD门限回归分析

阈值回归模型描述了一种简单的非线性回归模型。 TR规范很受欢迎，因为它们很容易。估计和解释，并能产生有趣的非线性和丰富的动力学。在TR的应用中，有样品分裂，多重平衡。非常流行的阈值自回归(TAR)和自激励阈值自回归(SETAR)(Hansen 1999, 2011;波特2003)。

在功能强大的特性中，Eviews有选择最佳阈值TR模型选择工具。能够从候选列表中，并且能够指定两种状态的变化和非变化的变量。例如，您可以轻松地指定两种模式的门限模型并允许EViews 估计最优变量和参数、阈值、系数和协方差。并对变化和回归参数的估计。

门限回归模型是一种重要的结构变化模型，当观测变量通过未知门限时，函数模型具有分段线性的特征，并且区制发生变化。门限回归模型很容易估计和解释，再加上它具备动态性，所以应用比较广泛。门限回归能够应用于多种模型中。

门限变量qt和解释变量Xt、Zt的特征决定了门限函数的类型。如果qt是yt的d期滞后值，则称为自激励（SE）模型；如果门限变量不是被解释变量的滞后变量，则为一般的门限回归（TR）模型。如果解释变量Xt、Zt中仅包含截距项和滞后的被解释变量，则表示自回归（AR）模型。在此基础上易于得出，自激励门限自回归（SETAR）模型中则包括自回归设定和滞后被解释变量两类要素。

Estimation Output

Criteria Graph and Table If you select View/Model Selection Summary from an estimated threshold equation you will be offered a choice of displaying a Criteria Graph or a Criteria Table:

BREAKLS带断点的最小二乘分析方法

基本普通最小二乘法假设模型的参数不随观测值的变化而变化。尽管这种假设。结构的变化，以及样本区间参数的变化，在应用时间序列分析中起着重要的作用。

因此，有大量的研究针对回归方程中参数结构变动的问题。EViews 8提出了结构变动的线性回归估计工具。在Bai (1997), Bai and Perron (1998)中的断点都是已知，先前指定的。

一、Estimating Least Squares with Breakpoints in EViews

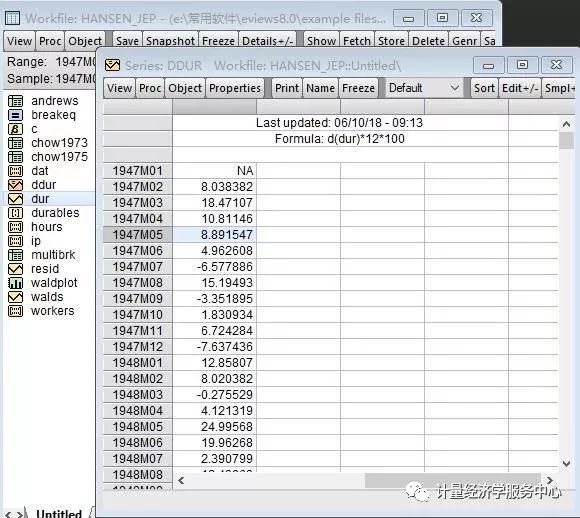
案例所需数据介绍，本节以hansen_jep为例，具体数据如下：

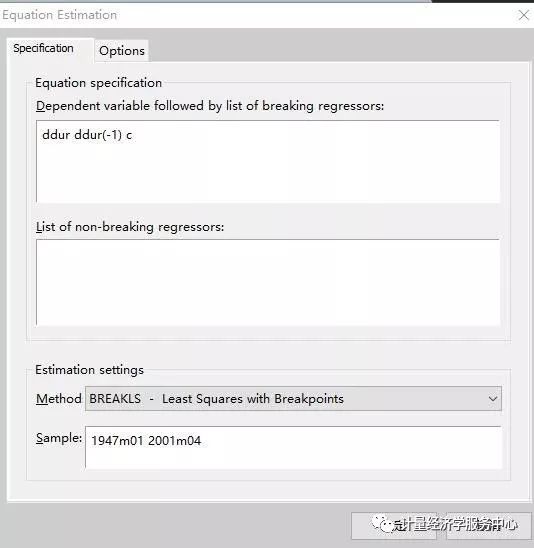
要估计一个具有断点的最小二乘方程，请选择Object/New Object….../ Equation or Quick/Estimate Equation，或者从EViews主菜单中选择BREAKLS - Method下拉菜单中带有断点的最小二乘法，或者在命令窗口中简单输入关键字BREAKLS:

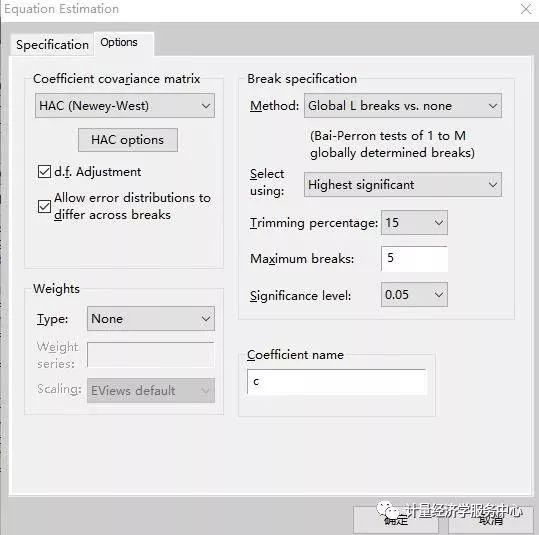
接下来，单击Options选项卡，显示计算系数协方差矩阵、断点说明、权重和系数名的附加设置。

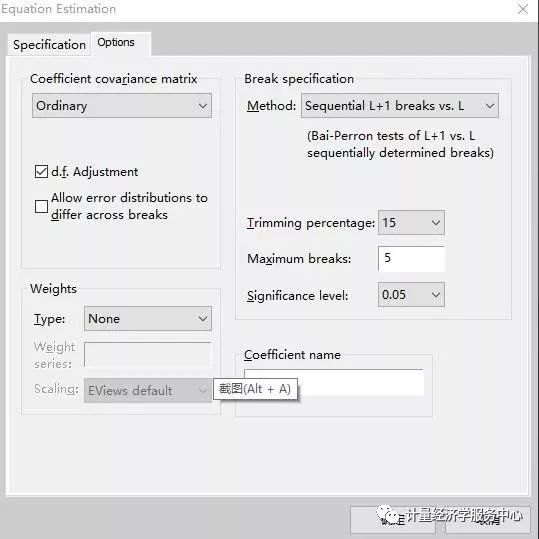
Break Specification包括如下选项：

The Break specification section of the dialog contains a Method drop-down where you may specify the type of test you wish to perform. You may choose between:

• Sequential L+1 breaks vs. L

• Sequential tests all subsets

• Global L breaks vs. none

• L+1 breaks vs. global L

• Global information criteria

• Fixed number - sequential

• Fixed number - global

• User-specified

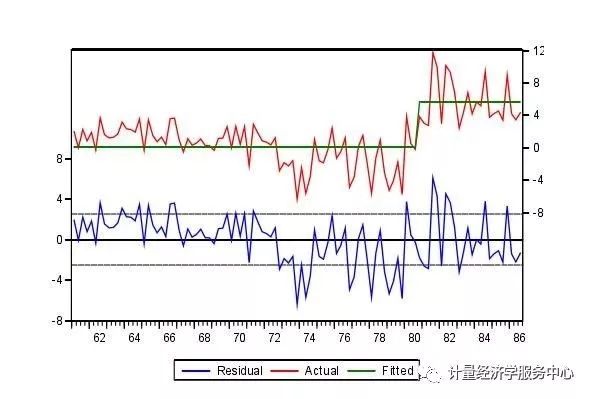
这些选项在结构突变检验章节将再次介绍。为了说明断点方程估计的输出，我们使用Han- sen’s (2001)劳动生产率的例子。Hansen的示例使用了1947年2月至2001年4月美国劳动生产率在制造业耐用品行业的测量。工业生产指数与每周平均工时之比增长率。

我们估计一个断点模型，使用DDUR与DDUR(-1)和一个常数的回归。输出如下:

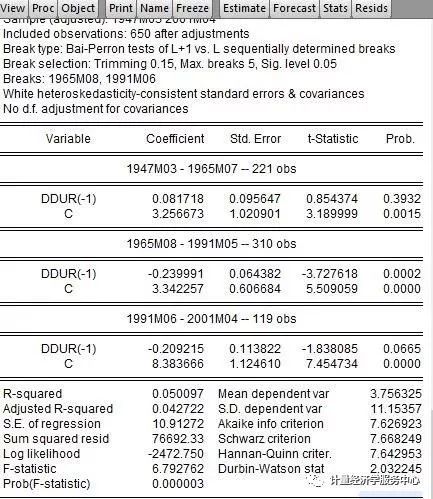
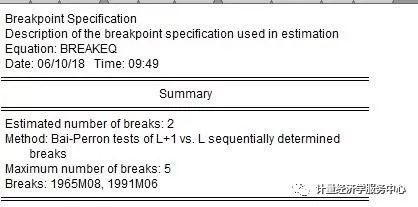
Breakpoint Specification View显示一个断点回归的总结,该方法用于确定断点。输出的顶部显示断点摘要以及剩下的部分显示了断点确定的中间结果:

二、Example

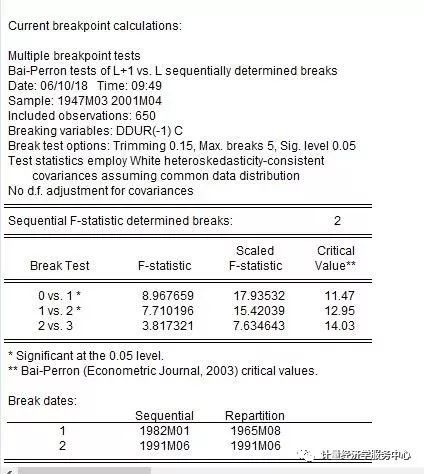
为了说明这些工具在实践中的使用，我们采用了美国出口实际利率的数据（from Garcia and Perron (1996) that is used as an example by Bai and Perron (2003a).）

选择对象/新对象…从主菜单中或在命令行中输入命令断点并单击enter。

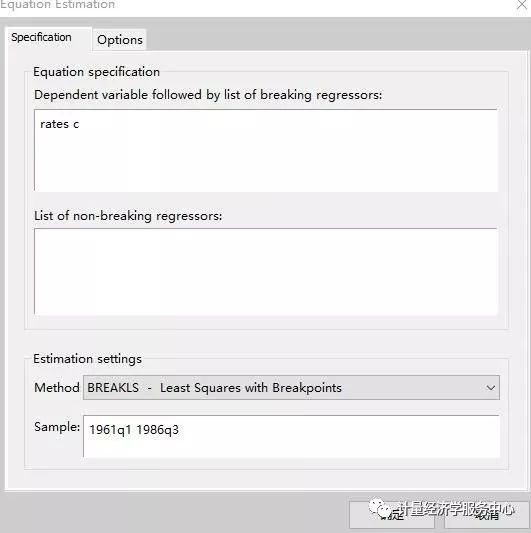
Next, click on the Options tab and specify HAC (Newey-West) standard errors, check Allow error distributions to differ across breaks, choose the Bai-Perron Global L breaks vs. none method using the Unweighted-Max F (UDMax) test to determine the number of breaks, and set a Trimming percentage of 15, and a Significance level of 0.05.

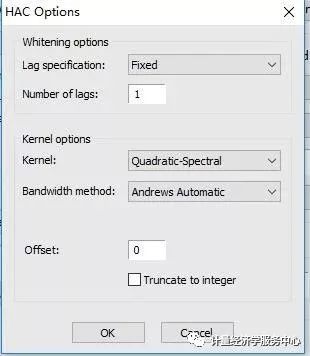
Lastly, to match the test example in Bai and Perron (2003a), we click on the HAC Options button and set the options to use a Quadratic-Spectral kernel with Andrews automatic bandwidth and single pre-whitening lag:

输出结果为：

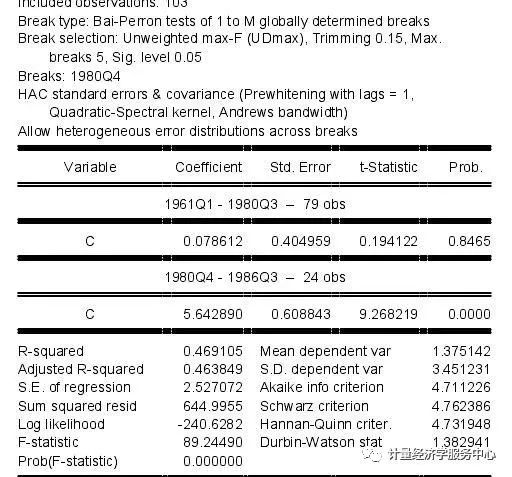
点击视图/实际，拟合，剩余/实际，拟合，残差图，在原始序列和残差的旁边，查看样本内的拟合数据: